研究紹介詳細表示
~自然科学の共通言語である数学を生かした異分野連携~
統計多様体の幾何学と統計モデリング
| 研究分野分類:4702 幾何学 産業分類:科学技術基礎,数理科学,数学教育 |
| キーワード:幾何学,統計数学,複雑系科学 |
| 数物系科学 |
| 数学 |
| 松添 博(情報工学専攻) |
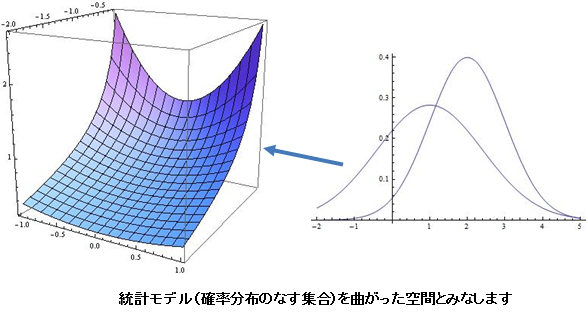
| 研究概要 曲線や曲面など、曲がった図形の概念を高次元化したものを「多様体」と呼びます。統計科学の分野では確率分布が重要な役割を果たしますが、統計モデル(確率分布の集まり)を高次元空間内の点の集まり、すなわち抽象的な図形である多様体とみなします。多様体論を用いて統計処理手法を考察します。 |
特徴 一般相対性理論では、質量があるとその周りの時空間が変化します。統計の幾何学では観測データに応じて情報空間が変化すると考えます。相対性理論に類似の発想ですが、極めて理論的と思われる数学、物理学が最先端の工学にも有用です。 |
|
| 背景・従来技術 近年のデータ科学は、特にビッグ・データ解析など、大自由度のパラメータから小自由度の有益な情報を取り出す必要がある問題が存在します。また、機械の故障確率など、極めて少数のデータから有益な情報を取り出す問題も存在します。従来の統計手法は、物理法則の検証など、多数の実験・観測から少数のパラメータを推定する場合に有効です。近年の統計科学には従来とは異なる新しい計算手法の構築が必要となります。 |
実用化イメージ 統計データ解析は工学や諸科学の共通基礎です。特定の分野や業種に限らず、自然科学の共通基礎として異分野連携が期待されます。 |

企業等への提案
研究者からのメッセージ
製品の開発法や計算機・インターネット環境などは近年大きく発展していると思います。その中で、解析手法として100年以上昔の数学を利用されていないでしょうか。最先端の抽象数学理論の必要性もご検討ください。
文献・特許
・Hiroshi Matsuzoe and Masayuki Henmi, Hessian Structures and Divergence Functions on Deformed Exponential Families, Geometric Theory of Information: Signals and Communication Technology (Springer), 2014, 57-80.
・Hiroshi Matsuzoe, Information geometry of Bayesian statistics, AIP conference proceedings, 1641(2014), 279-286
・Hiroshi Matsuzoe, Hessian structures on deformed exponential families and their conformal structures, Differential Geometry and its Applications, 35 Supplement, (2014), 323-333.
| 試作品状況 | 無し | 掲示可 | 提供可 |
| 共同研究を希望するテーマ 幾何学・統計学 数学教育(含企業) |
| 研究者データベースとのリンク(名前をクリックしてください) 研究者名:松添 博 |
| PDF表示と印刷 |



