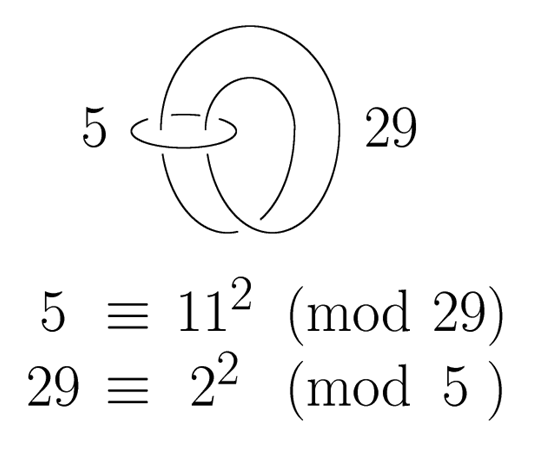研究紹介詳細表示
~数学と他分野との相互啓発~
高次元の素数と非可換な対称性の探求
| 研究分野分類:4701 代数学 産業分類:学校教育,その他の教育,学習支援業 |
| キーワード:整数論,ガロア理論,岩澤理論,数論的トポロジー,有限体 |
| 数物系科学 |
| 数学 |
| 水澤 靖(情報工学専攻) |
| 研究概要 高次元での素因数分解の難しさや複雑さを、そこに現れる高次元の素数たちの個性や相性により、非可換な対称性(ガロア群)として解明することを目指して研究しています。 |
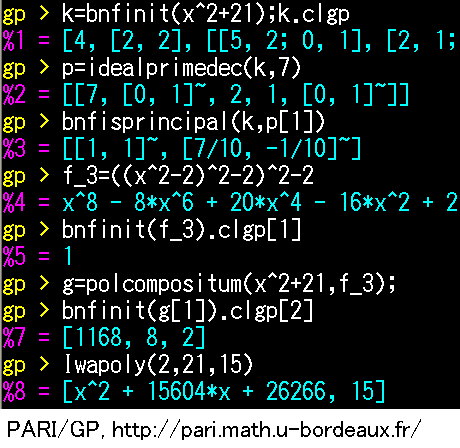
特徴 素数の個性を記述する理論(岩澤理論や有限体の理論など)を基盤として、計算機も援用しながら、素数と結び目(絡まった紐)の類似性(数論的トポロジー)の視点からも研究しています。特に、素数たちの2進的な個性や相性に着目した研究成果が多いです。また、新たな数学の研究テーマが派生することを期待して、誤り検査符号などの応用分野と関連する数学の研究にも注視しています。 |
|
| 背景・従来技術 現代の暗号セキュリティを支える基盤として素数判定や素因数分解の難しさなどがあり、また代数学(有限体の理論など)が誤り検査符号の理論においても応用されています。それらの応用の過程で登場した新たな対象が純粋数学の研究対象となり、新たな研究分野が派生することがあります。 |
実用化イメージ 他分野との専門的知識や興味の共有を通して、新たな研究分野や応用の芽が出ることを期待しています。 |
企業等への提案
研究者からのメッセージ
私たちがその恩恵を享受している科学の発展には、学問を学び受け継いできた多くの先人たちの貢献があることを、常に意識したいと思っています。
文献・特許
・Y. Mizusawa, Proc. Amer. Math. Soc. 138, 3095–3103 (2010)
・Y. Mizusawa, J. Théor. Nombres Bordeaux 22, 115–138 (2010)
・Y. Mizusawa et. al., Math. Z. 273, 1161–1173 (2013)
・Y. Mizusawa et. al., Finite Fields Appl. 25, 134–145 (2014)
・Y. Mizusawa, Ann. Math. Qué. 38, 73–79 (2014)
| 試作品状況 | 無し | 掲示可 | 提供可 |
| 研究者データベースとのリンク(名前をクリックしてください) 研究者名:水澤 靖 |
| PDF表示と印刷 |